Los Globals son espadas mágicas para almacenar datos. Parte 3. Matrices dispersas.
¡Hola a tod@s!
 En las partes anteriores (1, 2) de este artículo, hablamos de Globals como árboles. En esta tercera parte, los veremos como matrices dispersas.
En las partes anteriores (1, 2) de este artículo, hablamos de Globals como árboles. En esta tercera parte, los veremos como matrices dispersas.
Una matriz dispersa es un tipo de matriz donde la mayoría de los valores asumen un valor idéntico.
En la práctica, a menudo veréis matrices dispersas tan grandes que no tiene sentido ocupar memoria con elementos idénticos. Por lo tanto, tiene sentido organizar matrices dispersas de tal manera que no se desperdicie memoria al almacenar valores duplicados.
En algunos lenguajes de programación, las matrices dispersas son parte del lenguaje (por ejemplo, en J, MATLAB). En otros lenguajes, hay bibliotecas especiales que permiten usarlas. Para C ++, esos serían Eigen y similares.
Los Globals son buenos candidatos para implementar matrices dispersas por las siguientes razones:
- Solo almacenan valores de nodos particulares y no almacenan valores indefinidos;
- La interfaz de acceso para un valor de nodo es extremadamente similar a la que ofrecen muchos lenguajes de programación para acceder a un elemento de una matriz multidimensional.
Set ^a(1, 2, 3)=5 Write ^a(1, 2, 3) - Un Global es una estructura de nivel bastante bajo para almacenar datos, razón por la cual los Globals poseen características de rendimiento sobresalientes (cientos de miles a docenas de millones de transacciones por segundo dependiendo del hardware, ver 1)
Dado que una estructura Global es persistente, solo tiene sentido crear matrices dispersas sobre la base de situaciones en las que sabe de antemano que tendrá suficiente memoria para ellas.
Uno de los matices de la implementación de matrices dispersas es el retorno de un cierto valor por defecto si se dirige a un elemento indefinido.
Esto se puede implementar usando la función $GET en COS. Echemos un vistazo a una matriz tridimensional en este ejemplo.
SET a = $GET(^a(x,y,z), defValue)
Entonces, ¿qué tipo de tareas requieren matrices dispersas y cómo pueden ayudarlo los Globals?
Matriz de adyacencia
Tales matrices se utilizan para la representación gráfica:
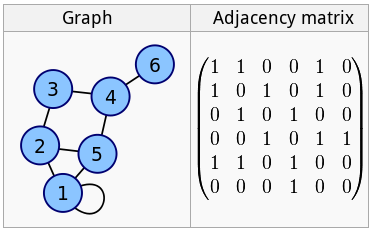
Es obvio que cuanto más grande es un gráfico, más ceros habrá en la matriz. Si miramos un gráfico de una red social, por ejemplo, y lo representamos como una matriz o este tipo, consistirá principalmente en ceros, es decir, será una matriz dispersa.
Set ^m(id1, id2) = 1
Set ^m(id1, id3) = 1
Set ^m(id1, id4) = 1
Set ^m(id1) = 3
Set ^m(id2, id4) = 1
Set ^m(id2, id5) = 1
Set ^m(id2) = 2
....
En este ejemplo, guardaremos la matriz de adyacencia en el global ^m, así como el número de bordes de cada nodo (quién es amigo de quién y el número de amigos).
Si el número de elementos en el gráfico no supera los 29 millones (este número se calcula como 8 * longitud máxima del string), Incluso hay un método más económico para almacenar tales matrices: cadenas de bits, ya que optimizan los espacios grandes de una manera especial.
Las manipulaciones con cadenas de bits se llevan a cabo con la ayuda de la función $BIT .
; setting a bit
SET $BIT(rowID, positionID) = 1
; getting a bit
Write $BIT(rowID, positionID)
Tabla de conmutadores FSM
Dado que el gráfico de conmutadores FSM es un gráfico regular, la tabla de conmutadores FSM es esencialmente la misma matriz de adyacencia de la que hablamos anteriormente.
Autómata celular

El autómata celular más famoso es "El juego de la vida", donde las reglas (cuando una celda tiene muchos vecinos, muere) esencialmente la convierten en una matriz dispersa.
Stephen Wolfram cree que los autómatas celulares son un nuevo campo de la ciencia. En 2002, publicó un libro de 1280 páginas llamado "Un nuevo tipo de ciencia", donde afirma que los logros en el área de autómatas celulares no están aislados, pero son bastante estables y son importantes para todos los campos de la ciencia.
Se ha demostrado que cualquier algoritmo que pueda ser procesado por una computadora también puede implementarse con la ayuda de un autómata celular. Los autómatas celulares se utilizan para simular entornos y sistemas dinámicos, para resolver problemas algorítmicos y para otros fines.
Si tenemos un campo enorme y necesitamos registrar todos los estados intermedios de un autómata celular, tiene sentido usar Globals.
Cartografía
Lo primero que me viene a la mente cuando se trata de usar matrices dispersas es la cartografía.
Como regla general, los mapas tienen mucho espacio vacío. Si imaginamos que el mapa mundial se compone de píxeles grandes, veremos que el 71% de todos los píxeles de la Tierra estarán ocupados por una matriz dispersa del océano. Y si solo agregamos estructuras artificiales al mapa, habrá más del 95% del espacio vacío.
Por supuesto, nadie almacena mapas como matrices de mapas de bits, todos usan la representación vectorial en su lugar.
¿Pero qué son los mapas vectoriales? Es una especie de marco junto con polilíneas y polígonos. En esencia, es una base de datos de puntos y relaciones entre ellos.
Una de las tareas más desafiantes en cartografía es la creación de un mapa de nuestra galaxia realizado por el telescopio Gaia. Hablando en sentido figurado, nuestra galaxia es un mamut de matriz dispersa : enormes espacios vacíos con puntos brillantes ocasionales: estrellas. Es 99,999999 .......% de espacio absolutamente vacío. Cache, una base de datos basada en Globals, fue seleccionada para almacenar el mapa de nuestra galaxia.
No sé la estructura exacta de Globals en este proyecto, pero puedo suponer que es algo así:
Set ^galaxy(b, l, d) = 1; star catalog number, if exists
Set ^galaxy(b, l, d, "name") = "Sun"
Set ^galaxy(b, l, d, "type") = "normal" ; Otras opciones pueden incluir un agujero negro, cuásar, enana roja y similar.
Set ^galaxy(b, l, d, "weight") = 14E50
Set ^galaxy(b, l, d, "planetes") = 7
Set ^galaxy(b, l, d, "planetes", 1) = "Mercury"
Set ^galaxy(b, l, d, "planetes", 1, weight) = 1E20
...
Donde b, l, d son coordenadas galácticas: latitud, longitud y distancia desde el sol.
La estructura flexible de Globals le permite almacenar cualquier característica de estrella y planeta, ya que las bases de datos globales no tienen esquemas.
Se seleccionó Caché para almacenar el mapa de nuestro universo no solo por su flexibilidad, sino también por su capacidad de guardar rápidamente un hilo de datos mientras se crean simultáneamente Globales de índice para una búsqueda rápida.
Si volvemos a la Tierra, se usaron Globals en proyectos centrados en mapas OpenStreetMap XAPI y FOSM, una bifurcación de OpenStreetMap.
Recientemente, en un hackathon de Caché, un grupo de desarrolladores implementó Geospatial indexes usando esta tecnología. Verr el artículo para mas detalles.
Implementación de índices geoespaciales usando Globals en OpenStreetMap XAPI
Se tomaron ilustraciones de esta presentación.
Todo el globo se divide en cuadrados, luego en subcuadros, luego en más subcuadros, y así sucesivamente. Al final, obtenemos una estructura jerárquica para la que se crearon Globals.

En cualquier momento, podemos solicitar instantáneamente cualquier cuadrado o vaciarlo, y todos los subcuadrados serán devueltos o vaciados también.
Un esquema detallado basado en Globals puede implementarse de varias maneras.
Variante 1:
Set ^m(a, b, a, c, d, a, b,c, d, a, b, a, c, d, a, b,c, d, a, 1) = idPointOne
Set ^m(a, b, a, c, d, a, b,c, d, a, b, a, c, d, a, b,c, d, a, 2) = idPointTwo
...
Variante 2:
Set ^m('abacdabcdabacdabcda', 1) = idPointOne
Set ^m('abacdabcdabacdabcda', 2) = idPointTwo
...
En ambos casos, no será un gran problema en COS/M solicitar puntos ubicados en un cuadrado de cualquier nivel. Será un poco más fácil limpiar segmentos cuadrados de espacio en cualquier nivel en la primera variante, pero esto rara vez se requiere.
Un ejemplo de un cuadrado de bajo nivel.:

Y aquí hay algunos Globals del proyecto XAPI: representación de un índice basado en Globals:

El Global ^way es utilizado para almacenar los vértices de polilíneas (caminos, ríos pequeños, etc.) y polígonos (áreas cerradas: edificios, bosques, etc.).
Una clasificación aproximada del uso de matrices dispersas en Globals.
- Almacenamos las coordenadas de algunos objetos y su estado (cartografía, autómatas celulares).
- Almacenamos matrices dispersas.
En la variante 2) cuando se solicita una determinada coordenada y no hay un valor asignado a un elemento, necesitamos obtener el valor predeterminado del elemento de la matriz dispersada.
Beneficios que obtenemos al almacenar matrices multidimensionales en Globals
Eliminación rápida y/o selección de segmentos de espacio que son múltiples de cadenas, superficies, cubos, etc.Para casos con índices enteros, puede ser conveniente poder eliminar rápidamente y/o seleccione segmentos de espacio que sean múltiples de cadenas, superficies, cubos y demás.
El comando Kill puede eliminar un elemento independiente, una cadena e incluso una superficie completa. Gracias a las propiedades de lo global, ocurre muy rápidamente, mil veces más rápido que la eliminación de elemento por elemento.
La ilustración muestra una matriz tridimensional en Global ^a y diferentes tipos de eliminaciones.
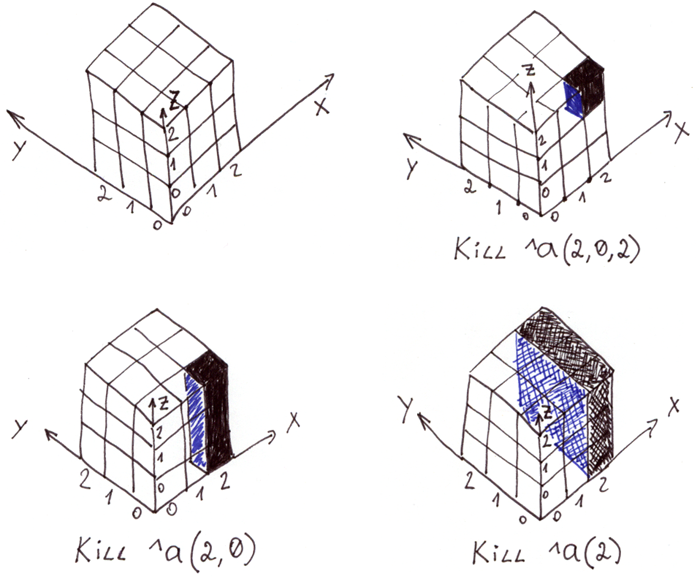
Para seleccionar segmentos de espacio por índices conocidos, puedes usar el comando Merge .
Selección de una columna de matriz en la variable Column:
; Let's define a three-dimensional 3x3x3 sparse array
Set ^a(0,0,0)=1,^a(2,2,0)=1,^a(2,0,1)=1,^a(0,2,1)=1,^a(2,2,2)=1,^a(2,1,2)=1
Merge Column = ^a(2,2)
; Let's output the Column variable
Zwrite Column
Output:
Column(0)=1
Column(2)=1
Lo interesante es que tenemos una matriz dispersa en la variable Column que puede abordar a través de $GET ya que los valores predeterminados no se almacenan allí.
La selección de segmentos de espacio también se puede hacer con la ayuda de un pequeño programa que utiliza la función $Order . Esto resulta especialmente útil en espacios con índices no cuantificados (cartografía).
Conclusión
Las realidades de hoy plantean nuevos desafíos. Los gráficos pueden consistir en miles de millones de vértices, los mapas pueden tener miles de millones de puntos, algunos incluso pueden querer lanzar su propio universo basado en autómatas celulares (1, 2).
Cuando el volumen de datos en matrices dispersas no puede exprimirse en la RAM, pero aún necesita trabajar con ellos, debe considerar implementar tales proyectos utilizando Globals y COS.
¡Gracias por su atención! Esperamos ver sus preguntas y solicitudes en la sección de comentarios.